JSER Policies
JSER Online
JSER Data
Frequency: quarterly
ISSN: 1409-6099 (Print)
ISSN: 1857-663X (Online)
Authors Info
- Read: 39546
|
МАТЕМАТИЧКИ ЈАЗИК ВО ОДДЕЛЕНСКА НАСТАВА
Јасмина КАРИЌ |
|
MATHEMATICS LANGUAGE IN-CLASS INSTRUCTION
Jasmina KARIKJ
Faculty of Special Education and |
|
|
|
|
|
Вовед |
|
Introduction |
|
|
|
|
|
„Математиката, соодветно гледана, содржи не самовистина, туку и огромна убавина“ |
|
“Mathematics, rightly viewed, possesses not only truth, but supreme beauty.” - Russell |
|
|
|
|
|
Математиката е начин за разбирање меѓу луѓето (1). Таа е форма на јазик, интернационален јазик, во кој комуницирањето се одвива по пат на симболи. За многу ученици совладувањето на јазикот во контекст на специфичните предмети е тежок процес. Учењето на математичкиот јазик не е возможно ако не се научат неговите зборови - математички термини. Едноставните, познати зборови кај учениците добиваат, повеќе или помалку неочекувани значења.
Ниту еден од овие начини не е правилен и не дава добри резултати. Во училиштата за глуви, покрај реализирањето на општите цели и задачи во наставата по математика, треба да се води сметка и за изведувањето на специфичните задачи, а тоа е создавање и развивање на говорот кај глувите деца преку наставата по математика, држејќи се до главниот принцип „учењето на јазикот е во с¢“ (8).
Содржината на говорниот материјал за секоја од трите групи е условена од одделението. Треба да се има предвид дека математичкиот речник на ученикот како средство за развој на неговото математичко мислење, ќе се развива само ако на него работиме систематски. |
|
Mathematics is a way of communication between people (1). It is a form of language – international language – in which symbols are used for communication. Mastering a language in the context of a specific subject is a tough process for many pupils. It is not possible to learn the language of mathematics without learning its words – mathematic terms. Simple words, known to pupils, in the mathematical context get new, more or less unexpected meanings.
Neither of these points was right and neither gave good results. In the schools for the hearing impaired, besides the realization of general goals and tasks of the mathematics instruction, the realization of specific tasks to create and develop speech in children who are hearing impaired using mathematics instruction should be noted, abiding by the main principle that “learning of the language is in everything” (8).
The content of the speech material is also conditioned by the individual class. We should bear in mind that a pupil’s mathematical vocabulary will only develop if it is systematically worked on, as a means of development of pupil’s thought. |
|
|
|
|
|
Методологија |
|
Methodology |
|
|
|
|
|
Целта на нашето истражување беше да се направи споредба на усвојувањето на математичкиот јазик кај учениците од пониските одделенија од специјалните основни училишта за деца со оштетен слух и учениците од редовните основни училишта. Поставени се и посебни цели со цел да се утврдат разликите според нивото на усвоеност на математичкиот речник меѓу учениците во однос на оштетувањето на слухот и во однос на возраста. |
|
The goal of the research was to compare the level in which mathematics knowledge was acquired in lower classes of special elementary schools for students who are hearing impaired compared to the level acquired in mainstream elementary schools. Special goals were set to determine the differences in accordance with the level in which mathematical vocabulary is acquired between pupils regarding hearing impairment and age. |
|
|
|
|
|
Инструменти и техники на истражување |
|
Research instruments and techniques |
|
|
|
|
|
За собирање на податоците за усвојување на математичкиот речник употребени се два теста, специјално конструирани тестови за истражувањето, наменети за испитување на математичкиот речник кои беа во склад со задачите формулирани во наставните планови и програми за испитуваните одделенија. Првиот тест е наменет за децата од прво одделение од редовните основни училишта и децата од прво и второ одделение во училиштата за глуви и наглуви. Вториот тест е наменет за децата од второ одделение од редовните основни училишта и децата од трето и четврто одделение во училиштето за глуви и наглуви. Тестовите содржеа точки кои се однесуваат на испитувањето на познавањето на математичките термини и симболи, како и математичките содржини соодветни за возраста. Тестирањето е извршено на овој начин заради аналогните наставни содржини. |
|
In order to gather data of the level mathematics language was acquired, two tests specifically developed for this research to test mathematics vocabulary were used, in accordance with the tasks stated in the curriculums and programs for the tested classes. The first test is intended for students in the 1st grade of a mainstream elementary school and students of the 1st and 2nd grade in a school for hearing impaired. The second test is intended for students in the 2nd grade of a mainstream elementary school and students in the 3rd and 4th grade in the school for hearing impaired. The tests included items related to testing familiarity with mathematical terms and symbols, as well as mathematical content appropriate for the age in question. The testing was done in this way because of the analogous curriculums. |
|
|
|
|
|
Примерок |
|
Sample |
|
|
|
|
|
Примерокот на истражување вклучува вкупно 239 ученици, од кои 188 ученици од 1-во и 2-ро одделение од редовните училишта во Белград (1-во одделение – 101 ученик, 2-ро одделение – 87 ученици) и 51 ученик од 1-во до 4-то одделение од основните училишта за деца со оштетен слух во Србија (1-во одделение – 14 ученици; 2-ро одделение – 12; 3-то одделение – 10; 4-то одделение – 15 ученици). Истражувањето е спроведено во текот на април 2009 година. |
|
The research sample included a total of 239 pupils. |
|
|
|
|
|
Резултати |
|
Results |
|
|
|
|
|
Успехот на учениците е изразен со проценти и даден е табеларен приказ на споредбената анализа на усвоеноста на математичкиот речник во 1-во и 2-ро одделение од училиштето за глуви и наглуви со 1-во одделение од редовните основни училишта (прв дел) и резултатите од 3-то и 4-то одделение од училиштата за глуви и наглуви со резултатите од 2-ро одделение од редовните основни училишта (втор дел). Ваквиот пристап во прикажувањето на резултатите е избран заради аналогијата на наставните содржини во овие одделенија. Според наставните планови и програми, математичките термини предвидени за 1-во одделение од редовните училишта се соодветни со математичките термини предвидени за 1-во и 2-ро одделение во училиштата за глуви и наглуви. Истото се однесува и за 2-ро одделение од редовните и 3-то и 4-то одделение од училиштата за деца со оштетен слух. |
|
A pupil’s success is shown using percentage points; tabular representation of comparative analysis of the acquisition of mathematics vocabulary in the 1st and 2nd grades of school for students who are hearing impaired compared to the 1st grade of mainstream elementary school (first part), and results from the 3rd and 4th grade of school for students who are hearing impaired compared to the results from the 2nd grade of mainstream elementary school (second part). This approach to the representation of results was chosen because of the analogy between curriculums in these grades. Namely, according to the curriculums, mathematical terms envisaged for the 1st grade of the mainstream elementary school coincide with the mathematical terms envisaged for the 1st and 2nd grades of the school for students who are hearing impaired. The same is true for the 2nd grade of the mainstream school and 3rd and 4th grade of the school for students who are hearing impaired. |
|
|
|
|
|
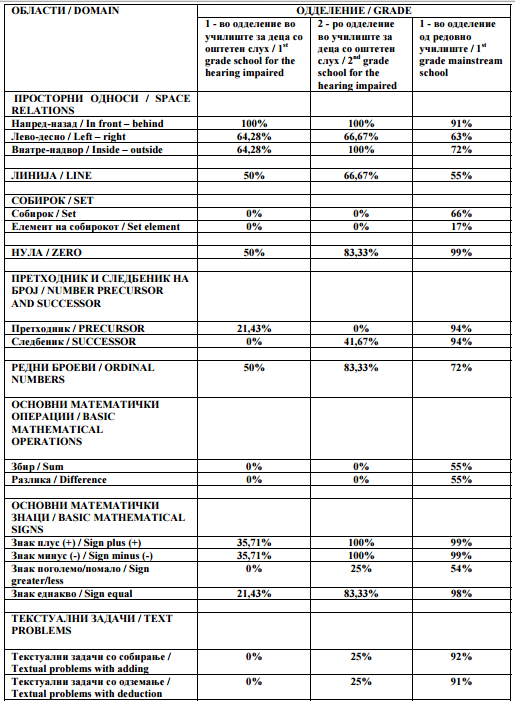
Прв дел Табела 1. Приказ на добиените резултати од испитувањето на математичкиот речник |
|
First Part Table 1. Acquired research results on the mathematics vocabulary testing |
|
Во поглед на усвоеноста на математичките термини потврдено е дека постојат разлики меѓу учениците од редовните училишта и училиштата за деца со оштетен слух. Најмали разлики се забележани во областа на линиите, каде учениците во приближно еднаков процент (околу половина) познаваат одредени линии. Учениците со оштетен слух од 2-ро одделение најдобро ги познаваат редните броеви. |
|
Regarding the acquisition of mathematical terms, this research confirms the existence of differences between pupils in mainstream schools and schools for students who are hearing impaired. The smallest differences were found in the field-domain of lines in part one of the table, where pupils in almost equal percent (about half) are familiar with certain lines. Pupils of the 2nd grade who are hearing impaired were most familiar with ordinal numbers. |
|
|
|
|
|
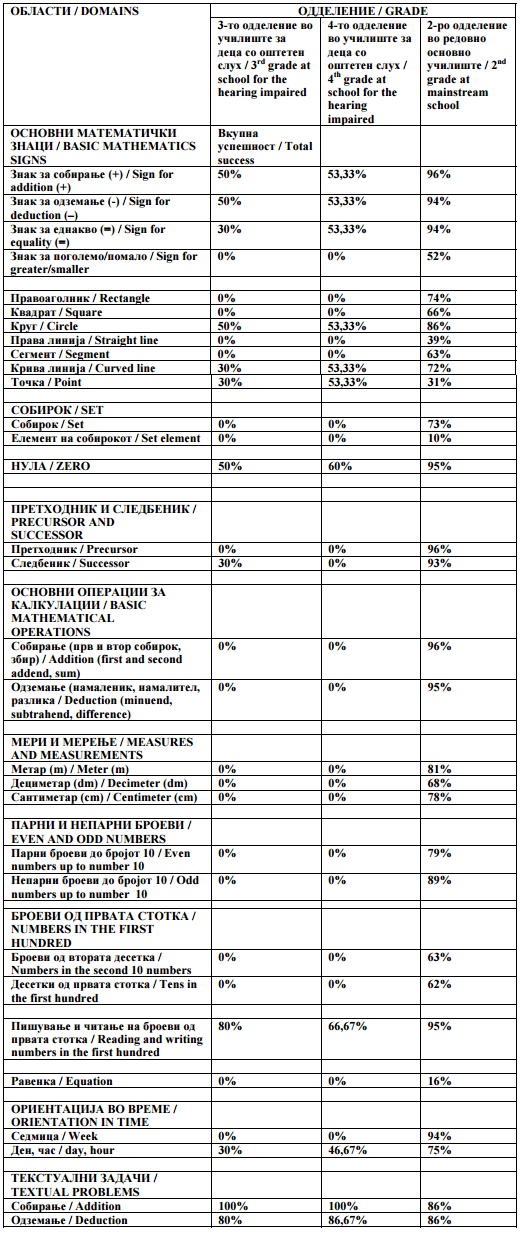
Втор дел Табела бр. 2 Приказ на добиените резултати од испитувањето на математичкиот речник |
|
Second Part Table 2. Acquired research results on the mathematics vocabulary testing |
|
При споредувањето на резултатите на учениците од 3-то и 4-то одделение во училиштата за глуви и наглуви ученици со 2-ро одделение од редовните основни училишта, пронајдени се многу големи разлики, неочекувано во корист на учениците од редовните училишта. Загрижувачки е тоа што учениците со оштетен слух и на оваа возраст и понатаму слабо ги познаваат математичките термини плус, минус, помало и поголемо.Претходно ги објаснив можните причини за ова, во интерпретацијата на резулататите. |
|
Much bigger differences were found when comparing the results of pupils in the 3rd and 4th grade of the school for the hearing impaired with the results of pupils of the 2nd grade of the mainstream school. Unexpectedly, this benefited mainstream school pupils. It is concerning that pupils who are hearing impaired, even at this age, are still not well familiar with the mathematic terms: plus, minus, less, and greater. We have previously stated probable causes for this in the interpretation of results. |
||
|
|
|
|
||
|
Дискусија |
|
Discussion |
||
|
|
|
|
||
|
Како што и очекувавме, помал број на ученици со оштетен слух решаваат текстуални задачи. Во примерите со текстуални задачи употребувани се зборови од секојдневниот говор, а целта не беше само учениците да ги решат задачите туку и да ги сфатат односите во задачите. Испитувани се и математички барања и термини: додади, одземи, вкупно и остаток. Лексичкиот фонд на децата со оштетен слух на оваа возраст е многу сиромашен, така што се претпоставува дека дури и да го знаат значењето на сите зборови, не се во состојба да го разберат граматичкиот облик на тие зборови. Меѓутоа тоа не е причина на учениците да не им се поставува овој вид на задачи во почетната настава по математика. |
|
As was expected, only a small number of pupils who are hearing impaired solved textual problems. In examples of textual problems, words from everyday speech were used – the goal was not only for the pupils to solve the problem but to understand the relations in the problem. Mathematical requests and terms were tested: to give, to take, total, and rest. Lexical fund for children of this age who are hearing impaired was very poor – so it was assumed that even if they know the meaning of all the words, they will not be able to understand grammatical forms of those words. But this does not give reason to refrain from teaching pupils this kind of problem in the beginning of mathematics instruction. |
||
|
|
|
|
||
|
ЗАКЛУЧОК |
|
CONCLUSION |
||
|
|
|
|
||
|
Ова истражување поттикна низа нови прашања и стари дилеми. Со оглед на фактот дека математичката писменост припаѓа на редот на секундарна писменост, се поставува прашањето колку децата со оштетен слух се математички писмени (15). Дали треба да се инсистира на изговарање на термините како плус или едноставно треба да им се дозволи на децата да говорот со „својот“ знаковен јазик? Ние сметаме дека е потребно и едното и другото, меѓутоа не во пониските одделенија. На оваа возраст треба постепено да се воведуваат децата во математичкиот јазик, овозможувајќи им да ги усвојат термините на јазикот кој најдобро го познаваат, без разлика дали е во прашање оралниот или гестовниот јазик. Подоцна, со развојот на говорот и апстрактното мислење децата треба покрај познавањето на термините да знаат како адекватно и да ги употребат. |
|
This research prompted a series of new questions and old dilemmas. Since mathematics literacy falls into the category of secondary literacy, the question arises as to how literate children who are hearing impaired are (15). Should it be insisted on that the term plus is spoken, or should children be left to simply say it with “their” sign language? We think both are needed, with the exception of lower grades. At this age, children should be gradually introduced to the language of mathematics and be allowed to acquire terms in a language that they understand best, be it oral or sign language. Later, with the development of speech and abstract thought, children should be able to adequately use and understand these terms. |
||
|
|
|
|
||
|
Citation:Karikj J, Radovanovikj SV. Mathematics Language in-Class Instruction. J Spec Educ Rehab 2010; 11(3-4):43-56. |
||||
|
|
||||
|
Литература / Bibliography |
|
|
||
|
|
|
|
||
|
1. Karikj J. Implikacije i ogranichenja za uchitelje i uchenike u primeni savremenih matematichkih metoda. Novi Sad: Pedagoshka stvarnost br. 9/10; 2006. p. 717-726. |
|
9. Aleksikj P. Formiranje pochetnih matematichkih pojmova. Beograd: Prosvetni pregled 11, prilog 9; 1974. |
||
Share Us
Journal metrics
-
 SNIP 0.059
SNIP 0.059 -
 IPP 0.07
IPP 0.07 -
 SJR 0.13
SJR 0.13 -
 h5-index 7
h5-index 7 -
 Google-based impact factor: 0.68
Google-based impact factor: 0.68
10 Most Read Articles
- PARENTAL ACCEPTANCE / REJECTION AND EMOTIONAL INTELLIGENCE AMONG ADOLESCENTS WITH AND WITHOUT DELINQUENT BEHAVIOR
- RELATIONSHIP BETWEEN LIFE BUILDING SKILLS AND SOCIAL ADJUSTMENT OF STUDENTS WITH HEARING IMPAIRMENT: IMPLICATIONS FOR COUNSELING
- EXPERIENCES FROM THE EDUCATIONAL SYSTEM – NARRATIVES OF PARENTS WITH CHILDREN WITH DISABILITIES IN CROATIA
- INOVATIONS IN THERAPY OF AUTISM
- AUTISM AND TUBEROUS SCLEROSIS
- DIAGNOSTIC AND TREATMENT OPTIONS IN AUTISTIC SPECTRUM DISORDERS – AN OVERVIEW
- THE DURATION AND PHASES OF QUALITATIVE RESEARCH
- REHABILITATION OF PERSONS WITH CEREBRAL PALSY
- DISORDERED ATTENTION AS NEUROPSYCHOLOGICAL COGNITIVE DISFUNCTION
- HYPERACTIVE CHILD`S DISTURBED ATTENTION AS THE MOST COMMON CAUSE FOR LIGHT FORMS OF MENTAL DEFICIENCY
















