|
Математичката писменост е од големо значење за нашето општество. Некои луѓе имаат проблеми при усвојувањето математички знаења и имаат тешки проблеми при обработката на бројки и магнитуди. Проценето е дека распространетоста на нарушувањето за усвојување математички операции (Mathematical Learning Disorders [MLD]) изнесува меѓу 2 и 16% од популацијата, во зависност од земјата на истражување и од употребените критериуми (1, 2). Имајќи предвид дека MLD е поврзано со трошоци за општеството, семејствата и за личноста, важно е подобро да се разбере причината за овој проблем при обработувањето броеви за да се развие ран третман што ќе се насочи кон основните причинители.
Постојат неколку модела во обидот да се опишат или да се објаснат механизмите за основниот квантитет на тешкотии за обработување на децата со MLD. Некои истражувачи сметаат дека проблемот на децата со MLD е резултат на специфично нарушување во основната нумеричка обработка (3,4). Според некои истражувања, децата со MLD побавно ги обработуваат малите броеви од нивните врсници со типичен развој (5). Сепак, не е постигнат консензус околу овој проблем, бидејќи другите истражувања не ги поддржуваат овие сознанија (6,7). Некои несовпаѓања можат да се објаснат со несимболичките стимули за бројот или со точкестите прикази употребени во истражувањата. Поставена е хипотеза за постоење систем за „мали“ и систем за „големи“ броеви. Сепак, податоците за обработување „мал“ број и за „границата“ меѓу малите и големите броеви, се оскудни.
Бројките се инхерентно присутни во секојдневниот живот дури и кај многу малите деца. Изложеноста на квантитет започнува многу рано. Истражувањата за предвербалните деца откриле дека кај доенчињата се среќаваат два система за обработка на броевите (8-10). Првиот систем е објектно-датотечен систем, којшто дозволува точно претставување на ограничен број ставки (11, 12). Со овој систем се предлага за поставките до четири, доенчињата да можат да кореспондираат со еден на еден за секоја ставка, што овозможува прецизна дискриминација во рангот на малите броеви. Вториот систем е систем на аналогна магнитуда што дава понепрецизно, приближно претставување на поголемите броеви (9). Во овој случај, бројната дискриминација зависи од размерот, што значи дека негово клучно својство е релацијата меѓу два броја. Поголемо растојание меѓу броевите (како резултат на зголемениот размер) значи полесна дискриминација. Двосистемскиот профил е поддржан со поставување лимит на големини кај објектно-датотечниот систем што функционира како референтна точка за определување на границата меѓу опсегот на мали и големи броеви (13,14).
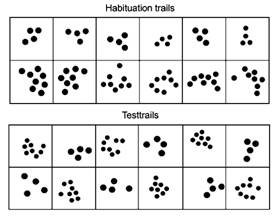
Обработката на нумеричката магнитуда е често истражувана кај доенчиња со хабитуациската парадигма (10, 14-20). Задачите според оваа парадигма се потпираат на хабитуацијата на одреден број ставки во текот на една фаза. За оваа задача децата гледаат одреден број стимули (на пр., приказ на точки) сѐ додека не се навикнат на нив (или не достигнат максимален број хабитуациски обиди, најмногу 14). Потоа тие го гледаат, наизменично, истиот број и новиот број. Дисхабитуацијата (или помалку гледање) на стариот број или подолго гледање во новиот број во текот на одредена фаза од тестирањето се смета како индикација за дискриминација (или воочување на разликата) на броевите. Што се однесува до објектно-датотечниот систем, претходните истражувања илустрираат поставен лимит на големини на три ставки. Овие истражувања оценуваат дека доенчињата не можат да разликуваат четири ставки од мали броеви во размер 1:2, 2 vs. 4 (10). Тие, сепак, ги разликуваат оние ставки од големи броеви поставени со ист размер, 4 vs. 8 (10). Заедно со неуспехот за разликување три ставки од големи броеви во размер 1:2, 3 vs. 6 (12), се претпочита лимитот на објектно-датотечниот систем да биде три за доенчињата. Според тоа, поставеноста на три и помалку е категоризирана во рамките на „мали“ броеви, додека поставеноста што го надминува ова ограничување е опфатена во рамките на „големи“ броеви (10, 15). 6-месечни бебиња ги разликуваа големите броеви во размер 1:4, 4 vs. 16 (19); 1:3, 7 vs. 21 (20) или 1:2, 4 vs. 8, 8 vs. 16, 16 vs. 32 (10, 15, 17, 19, 21). Разликувањето не беше возможно во размер 2:3, 8 vs. 12, 16 vs. 24 (15, 18). Исто така беа истражувани и комбинации од мали и големи броеви. Сепак, сѐ уште не е постигнат консензус. Истражувањата не дадоа позитивни резултати за разликување на комбинациите од броевите 2 vs. 4 (10, 11) и 3 vs. 6 (12), во чиишто рамки броевите беа претставени во размер 1:2. Овој неуспех се објаснува со некомпатибилноста на форматите за претставување бидејќи малата поставеност (во овој случај два и три) е претставена од објектната датотека, а големата поставеност од аналогната магнитуда (во овој случај четири и шест). Поради ова, невозможно е да се споредат два претставени броја во различни комбинации. Оваа некомпатибилност, сепак, не го објаснува успешното разликување на малите и големите броеви, како што е покажано за 7-месечни доенчиња при поставеноста 1 vs. 4 (12). Авторите, затоа, ја предложија хипотезата за прагот, според која е потребен минимален праг на промена за да можат доенчињата да ја разликуваат малата од големата поставеност. Според ова, доенчињата би можеле да ги игнорираат објектните датотеки и да се раководат само според аналогната магнитуда кога размерот меѓу малите и големите броеви го достигнува критичниот праг од 1:4 (или можеби дури и 1:3).
Така, еден начин за објаснување на разликувањето на една од четирите ставки е дека комбинацијата 1 vs. 4 е целосно обработена од системот на аналогни магнитуди. Сепак, друго објаснување е одредувањето на лимитот на големината на објектно-датотечниот систем, сугерирајќи дека 4 може да биде „мал“ број обработен од објектната датотека. Неодамнешните истражувања покажаа успешно разликување во комбинациите 1 vs. 3 (22) и 2 vs. 3 (16), поддржувајќи ги конкретните карактеристики на објектно-датотечниот систем. Сепак, овој систем може да ги изброи само броевите до четири (23, 24). Затоа може да се доведе во прашање дали 4 е „мал“ или „голем“ број и дали одредувањето на големината може да биде повисоко отколку што се претпоставувало (10, 15).
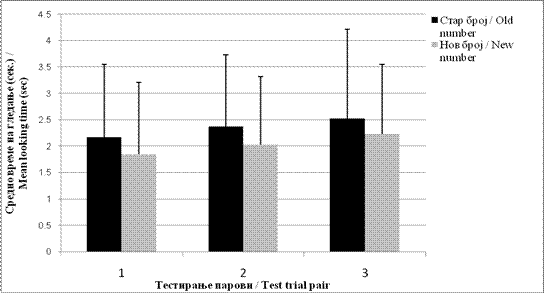
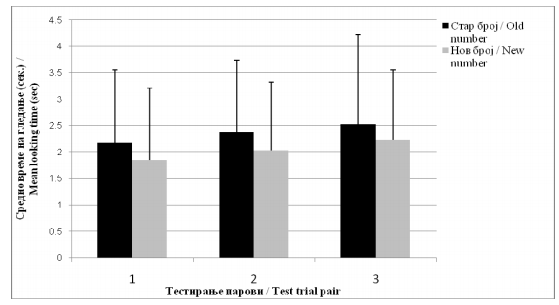
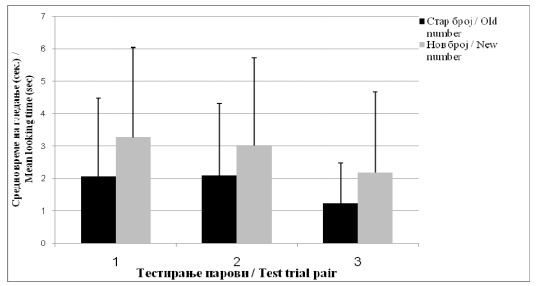
Целта на ова истражување е да испита дали бројот 4 е „мал“ или „голем“ број со две претходно испитувани комбинации со бројот 4 со мали и големи броеви, соодветно. Во првиот експеримент, во текот на хабитуациската задача 9-месечните бебиња треба да ги разликуваат 4 и 8 (со претпоставка дека се „големи“ броеви). Оваа комбинација на броевите претходно била успешна за 6-месечните бебиња (18). Следствено, се очекуваше и овојпат учесниците да покажат успех. Во вториот експеримент, друга група 9-месечни бебиња имаа хабитуациска задача за 1 vs. 4. Неодамна Cordes и Brannon (12) открија дека 7-месечните бебиња прават разлика меѓу овие броеви.
Доколку доенчињата успешно ги решат овие комбинации, тогаш бројот 4 може да се смета за „голем“ број во согласност со претходните истражувања (10). Дополнително може да се потврди хипотезата за прагот (12). Ако за 1 vs. 4 не се добие позитивен резултат, а се добие за 4 vs. 8, тогаш 4 е голем број без потврдување на хипотезата за прагот. А доколку 4 може да се разликува од 1, но не може да се разликува од 8, тогаш може да се обработува како „мал“ број.
Ова истражување го разгледува ова прашање со поголем примерок (N ≈ 25 наместо N = 16) и со посоодветни методи од претходните (10, 17). Понатаму, одлуката за тоа каде гледа детето (за да се измери времето на гледање) во ова истражување се базира на снимање на вкочанетиот поглед на детето, наместо со снимање на правецот на лицето на доенчето со VCR. Ова може да придонесе за подобар увид во способностите за разликување мали броеви кај доенчињата. Во доменот на превенцијата, со овие подобрени сознанија може да се обезбеди рана детекција на индивидуалните разлики. Следствено, ќе може да се направи разлика меѓу ризични деца и деца со типичен развој. Повеќе информации за овој метод се дадени во поврзаниот дел.
|
|
Mathematical literacy is important in our society. Some individuals have problems acquiring mathematical literacy and remain having severe problems to process numbers and magnitudes. The estimated prevalence of Mathematical Learning Disorders (MLD) lies between 2 and 16% of the population depending on the country of the study and the used criteria (1, 2). Given that MLD is associated with cost to society, family and the individual person, it is important to understand better what causes these problems in number processing so that early treatments can be developed and targeted at the underlying causes.
There are several models trying to describe or explain the mechanisms underlying quantity processing deficits in children with MLD. Some researchers consider the problems of children with MLD as the result of a specific disorder in basic numerical processing (3, 4). According to some studies, children with MLD are slower elaborating small numbers compared to typical achieving peers (5). However, there is no consensus on this problem since other studies do not support this finding (6, 7). Some of the inconsistencies might be explained by the number of non-symbolic stimuli or dot collections used in studies. It has been hypothesized that there is a system for ‘small’ and a system for ‘large’ numbers. However, data on ‘small’ number processing and on the ‘boundary’ between small and large numbers are scarce.
Numbers are inherently present in everyday life even in very young children. The exposure to quantities starts quite early. Studies on preverbal children revealed that infants rely on two systems to process numbers (8-10). The first system is an object-file system, which allows an exact representation of a limited number of items (11, 12). This system proposes that for sets of up to four, infants have an exact one-to-one correspondence representation of the items, allowing precise discrimination in the small number range. The second system is an analogue magnitude system that enables a less precise, approximate representation of larger numbers (9). In this case, number discrimination is ratio-dependent, meaning that the relation between two numbers is its key feature. The larger the distance between the numbers (as a result of an increasing ratio), the easier the discrimination. The two-system account is supported by the set size limit of the object-file system, which functions as the reference point for defining the boundary between the small and large number range (13, 14).
Numerical magnitude processing has often been studied in infants using a habituation paradigm (10, 14-20). Tasks according to this paradigm rely on habituation to a number of items during one phase. In these tasks children see a specific number of stimuli (e.g., a collection of dots) until they are habituated to it (or had a maximum number of habituation trials, mostly 14). Afterwards, they see, in alternating order, the same number and a new number. Dishabituation (or less looking) to the old number or longer looking at a novel number during a test phase are considered as an indication of discriminating (or seeing the difference) between the numbers. Regarding the object-file system, previous studies illustrated a set size limit of three items. Those studies revealed that infants could not discriminate four items from a small number in a 1:2 ratio, 2 vs. 4 (10). They did, however, discriminate those items from a large number in a set with the same ratio, 4 vs. 8 (10). Together with the failure of discriminating three items from a larger number in a 1:2 ratio, 3 vs. 6 (12), the limit of the object-file system is supposed to be three for infants. Set sizes of three and fewer are, therefore, categorised within the ‘small’ number range, while set sizes exceeding this limit are situated within the ‘large’ number range (10, 15). Large numbers were discriminated by 6-month-olds within a ratio of 1:4, 4 vs. 16 (19); 1:3, 7 vs. 21 (20) or 1:2, 4 vs. 8, 8 vs. 16, 16 vs. 32 (10, 15, 17, 19, 21). Discrimination was not possible in a 2:3 ratio, 8 vs. 12, 16 vs. 24 (15, 18). Combinations including a small and a large number were also investigated. Though, a consensus has not been reached yet. Studies did not find positive results for the discrimination of the number combinations 2 vs. 4 (10, 11) and 3 vs. 6 (12), in which numbers were presented in a 1:2 ratio. This failure was explained by the incompatibility in representational formats since small sets (in this case two and three) were represented by object files and large sets by analogue magnitudes (in this case four and six). This would make it impossible to compare the two presented numbers within the different combinations. This incompatibility, however, cannot explain the successful discrimination of the small from a large set as shown by 7-month-olds in 1 vs. 4 (12). The authors, therefore, proposed the threshold hypothesis according to which a minimum threshold of change is needed for infants to discriminate a small from a large set. Following this account, it might be possible for infants to ignore the object files and solely use analogue magnitudes when the ratio between a small and a large set exceeds a critical threshold of 1:4 (or maybe even 1:3).
Therefore, one way of explaining the discrimination of one from four items is that the combination 1 vs. 4 is entirely processed by the analogue magnitude system. However, another explanation is the set size limit of the object-file system by suggesting that four might be a ‘small’ number processed by object-files. Recent studies have shown successful discrimination for the combinations 1 vs. 3 (22) and 2 vs. 3 (16), supporting the precise-characteristic of the object-file system. However, this system can account for number sets up to four (23, 24). It can, therefore, be questioned whether four is a ‘small’ or a ‘large’ number and whether the set size limit might be larger than previously assumed (10, 15).
This study aims to investigate whether four is either a ‘small’ or a ‘large’ number, with two previously studied number combinations combining the number four with a small and a large number, respectively. In the first experiment 9-month-olds need to discriminate four and eight (assumed to be ‘large’ numbers) during a habituation task. This number combination was previously successful in 6-month-olds (18). Consequently, participants were expected to succeed. In the second experiment, another group of 9-month-olds received the 1 vs. 4 habituation task. Recently, Cordes and Brannon (12) found that 7-month-olds could discriminate between those numbers.
If infants are successful in both combinations, four can be categorized as a ‘large’ number in line with previous studies (10). In addition, the threshold hypothesis (12) can be confirmed. If 1 vs. 4 is not successful but 4 vs. 8 is, thеn four is likely to be a ‘large’ number without confirming the threshold hypothesis. If however, four can be discriminated from one but not from eight, four might be processed as a ‘small’ number.
The current study addressed this issue with a larger sample (N ≈ 25 instead of N = 16) and a more accurate method than previous ones (10, 17). Furthermore, the decision of where a child was looking (to measure looking times) in this study was based on the recording of the infant’s gaze by eye-tracking instead of the recorded direction of the infant’s face by a VCR. This might help to reach a better insight in the ability of discriminating small numbers in infants. Within the scope of prevention early detection of individual differences may be established by this better knowledge. Consequently, it might be possible to distinguish children at risk from typical developing children. More information on this method is given in the related section.
|
|
Во ова истражување учествуваа учесниците од едно поголемо лонгитудиално истражување. „Деца и семејство“ (Dutch: Kind en Gezin; http://www.kindengezin.be), владина агенција одговорна за малите деца и семејствата во Фландрија ги информираа родителите на децата родени меѓу мај 2008 и април 2009 година, коишто живеат во различни делови во Фландрија, Белгија. Од родителите што пополнија согласност за информираност, 10% беа поканети, по случаен избор, со информативно писмо за учество во дополнително мултидисциплинарно лонгитудинално истражување, од коешто е дел и ова истражување. Истра-жувањето беше спроведено на клиниката „Деца и семејство“. Родителите беа телефонски контактирани за состанок, доколку се согласиле.
Ова истражување вклучува 25 доенчиња, 10 машки и 15 женски, на возраст од 33 до 38 недели (M = 36,32 недели, SD = 1,55), коишто учествуваа во првиот експеримент (4 vs. 8). Понатаму, на 26 доенчиња (14 машки и 12 женски) на иста возраст (M = 35,73 недели, SD = 1,56) им беа дадени задачи за вториот експеримент (1 vs. 4).
Дванаесет доенчиња беа исклучени од истражувањето поради софтверска грешка во текот на тестирањето (n = 8), недоволно собирање податоци како резултат на вознемиреност (n = 2) или отсуство на внимание (n = 1) и поради губење на податоците на компјутерот по тестирањето (n = 1).
|
|
Participants for this study were recruited within the scope of a larger longitudinal study. Child & Family (Dutch: Kind en Gezin; http://www.kindengezin.be), a governmental agency with responsibility for young children and families in Flanders informed parents of children born between May 2008 until April 2009 and living in different districts in Flanders, Belgium. From the parents who filled out an informed consent, 10% were randomly invited with an informative letter to participate in an additional multidisciplinary longitudinal study, of which this study is one part. The research moments took place at clinics of Child & Family. Parents were contacted by phone for appointments if they consented.
The study reported here included 25 infants, 10 boys and 15 girls, aged between 33 and 38 weeks (M = 36.32 weeks, SD = 1.55) which were assigned to the first experiment (4 vs. 8). Furthermore, 26 infants were included (14 boys and 12 girls) with the same age range (M = 35.73 weeks, SD = 1.56) who were assigned to the second experiment (1 vs. 4).
12 infants were excluded from the study because of software failure during testing (n = 8), insufficient data collecting due to fussiness (n = 2) or inattentiveness (n = 1) and loss of the data on the computer afterwards (n = 1).
|
 SNIP 0.059
SNIP 0.059 IPP 0.07
IPP 0.07 SJR 0.13
SJR 0.13 h5-index 7
h5-index 7 Google-based impact factor: 0.68
Google-based impact factor: 0.68